2022. 1. 26. 15:56ㆍ주식공부/투자원칙 철학
펀더멘탈 vs 밸류에이션 - 쎈회사가 싼회사보다 좋은 이유
1. 국내 대형 건설사의 PBR밴드 주가가 눈에 딱 들어오고, 지금 과거기준으로 봤을 때 저평가 영역이다....
blog.naver.com
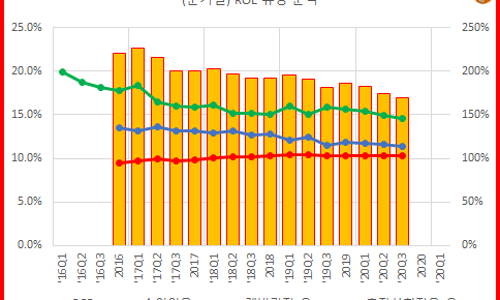
쎈회사를 판단할 수 있는 가장 중요한 '지표'는 지속가능한 ROE 수준이라고 생각하는데,
이 지속가능한 ROE라는 거 자체가 매우 주관적인 지표다.
공부를 많이 해야 하고.
ROE = 당기순이익 / 자기자본
좀 더 들여다보면 그렇게 단순하지가 않다.
당기순이익은 flow 를 측정하고, 자기자본은 stock을 측정하기 때문에 시차가 생긴다.
ROE
= 순이익(Net Income during t=0 ~ t=1) / 기초 자기자본(BV at t=0)
= NI_1 / BV_0
시점 t=1에서 가격(시가총액)을 P_1이라고 하면,
ROE = NI_1 / BV_0 에서 분자분모를 가격으로 나눈다.
그러면,
ROE = (NI_1 / P_1) / (BV_0 / P_1)
분자인 NI_1 / P_1 = 순이익 / 주가 = 1/ PER_1 이 되고,
분모는 BV_0 / P_1 = 기초 순자산 / 기말 주가
PBR = 가격 / 순자산인데 같은 시점에서의 가격과 순자산이라고 봐야할 것이기에..
기초 순자산 / 기말 가격 은 엄밀히 말하면 PBR은 아니다.
ROE = PBR / PER 이라고 하는 것은 시점까지 따져보면 좀 애매하게 틀린 식이 될 수도 있는데..
뭐 여기까진 따지지 않기로 하고.
ROE = PBR / PER 에서 시작해본다.
흔히, ROE-PBR 플롯팅에서 기울기는 PER(=PBR/ROE)이 된다.
버틀러의 <분석>탭에 있는 ROE-PBR 그래프가 이것인데,
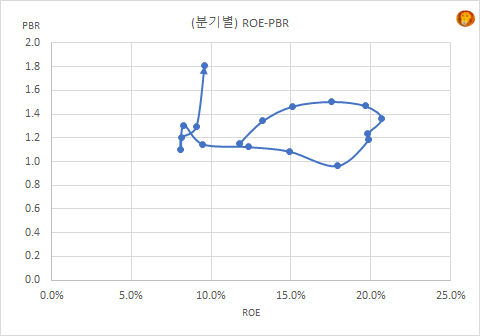
ROE 는 기업의 펀더멘탈,
PBR은 주가의 밸류에이션이라고 볼수 있고,
기울기가 PER이 된다.
삼성전자의 경우,
ROE가 10% 변할 때, PBR은 0.6(1 <-> 1.6)이 변화한다고 볼 수 있고.
PER = PBR/ROE에서 PER의 변화량은 PBR 변화량보다 6배 정도 된다고 볼 수 있다.
사이클 사이에서 PBR은 1~1.6, PER은 5~20 배를 오간다.
대충 관계 정도만 이해하면 될 것 같고,
보고자 하는 것은,
ROE = PBR / PER 에서..
기업의 장기 펀더멘탈, PBR밴드에서 밴드의 변화를 이해해 보고자 한다.
P(주가, 시가총액)
= BV (book value, 순자산=자본)x PBR
= NI (net income, 순이익) x PER
주가는 순자산을 시장이 평가하는 가치인 PBR을 곱해서 구할 수 있고,
또한 이익에 대해서도 시장이 평가하는 가치인 PER을 곱해서 구할 수 있다.
순자산은 회사의 미래 이익의 원천이기 때문에,
PBR이 1보다 크다는 얘기는 이 회사의 재무제표상 자산의 가치에 비해 미래에 이 회사가 벌어들일 돈에 대한 기대치가 크다는 것을 의미할 것이고,
1보다 작다는 얘기는 상대적으로 미래 이익에 대한 기대치가 작다는 것을 의미한다.
한가지 가정을 해보면,
시장의 PER 은 ROE에 비례하다고 보고,
PER = ROE x 100으로 둔다.
ROE가 10%인 회사는 PER 10배,
20%인 회사는 20배.
5%인 회사는 5배.
이렇게 하면 자산의 가치를 반영하지 못하긴 하지만,
현실에는 어느정도 부합한다고 본다.
그러면,
PBR = ROE x PER에서 계산이 된다.
배당성향을 d,
지속가능한 순이익성장율을 g라고 하면,
g = 지속가능한 ROE x (1-d) 가 된다.
이걸로 기업의 순자산의 변화와 시가총액의 변화를 시뮬레이션 해본다.

바꿀 수 있는 변수들은 위의 네가지가 되고,
그 결과로 지속가능한 ROE 가 결정된다.
sROE(sustainable ROE) = g/(1-d)
먼저, 배당성향과 배당소득세를 모두 0이라고 둔다.
순이익성장율과 ROE가 같으면 sROE = g 가 된다.
자본이 성장하는 만큼, 시가총액도 같이 성장한다.
ROE를 10%로 유지하려면 성장이 10% 필요하다는 얘기.
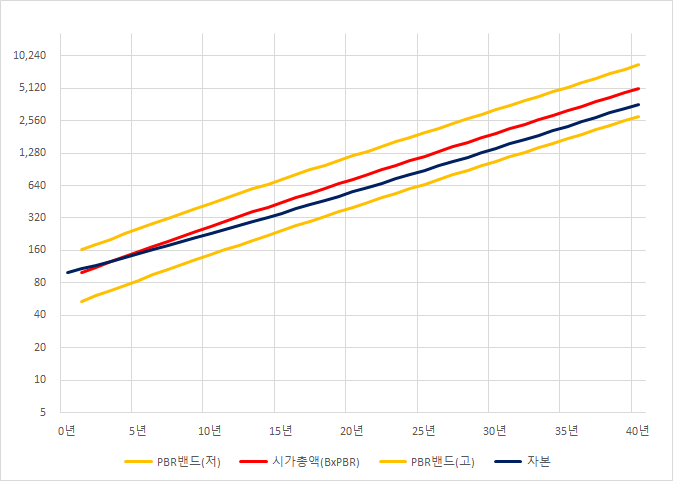
현재 시총은 100 (자본 100, PBR=1)
기업이 현재의 상황을 꾸준히 유지한다면 주가는 1년에 10% 상승.
40년간 기업의 변화와 주가를 시뮬레이션 해보면,
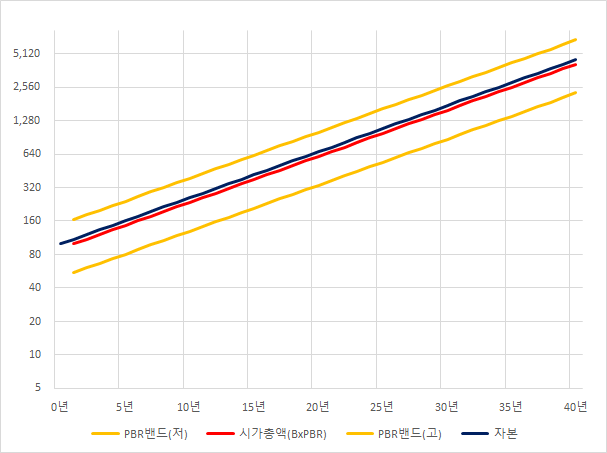
(좌축은 log)
밴드는 0.5xPBR(저), 1.5xPBR(고)
이번에는 성장율과 현재 ROE를 5%로 낮춰본다.
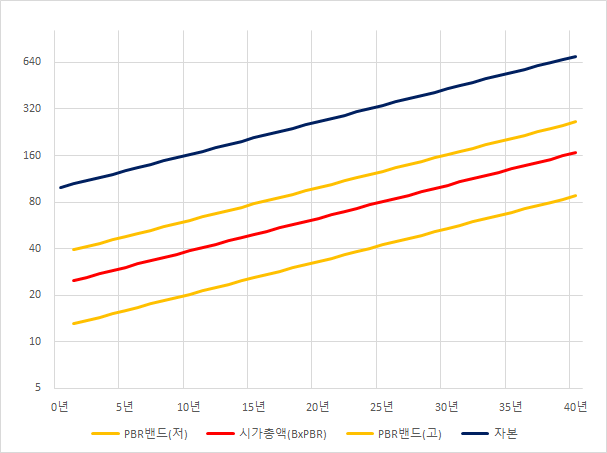
성장의 속도가 절반이 되면,
PER = ROE x 100 = 5
PBR = ROE x PER = 0.25
시가총액은 25로 4분의 1이다.
앞으로 기업에 변화가 없다면 주가도 연평균 5%로 상승.
이런 경우,
위의 ROE=10인 회사에 비해 '싸다'라고 느끼는 투자자들이 많을 것이고,
'가치투자'라고 불리기 쉽다.
버는 돈은 절반인데, 가격은 4분의 1이니까.
그런데,
기업의 변화가 없을 경우,
지금의 밸류에이션은 앞으로도 유지가 될 것이고,
그 경우에 주가는 ROE가 높은 회사가 더 오르게 된다.
계속해서 다른 숫자로 시뮬레이션.
이번에는,
성장율과 현재의 ROE를 20%로 올려본다.
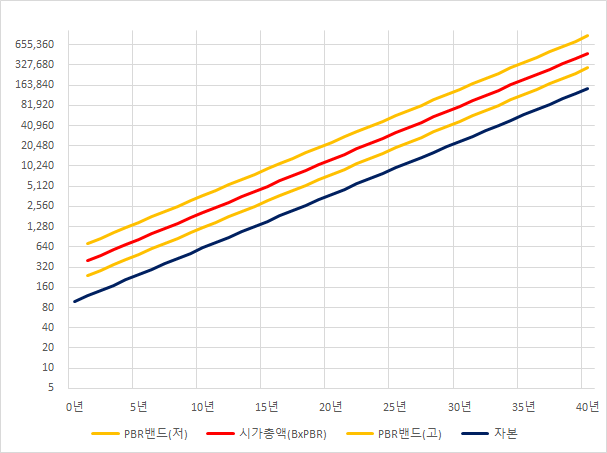
그러면 현재의 시가총액은 400으로,
ROE가 10%일때의 4배가 된다.
기업의 영위하는 업이 유지가 된다는 가정하에서,
장기적으로 투자자의 투자수익율은 ROE와 같아진다.
ROE가 높은 회사의 투자수익율이 높을 수밖에 없다.
이번에는 기업에 변화가 생기는 경우를 본다.
현재 10%의 ROE인 회사의 성장율이 20%로 올라갈 경우.
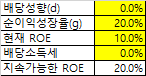
순이익 성장이 장기적으로 20%로 유지될 수 있다면,
이 회사의 sROE수준도 20%로 올라가게 된다.
현재 PER = 10이된 회사는 PER이 20을 향해 올라가게 되고,(리레이팅)
가격의 변화는 기업의 변화 초기에 반영되게 된다.
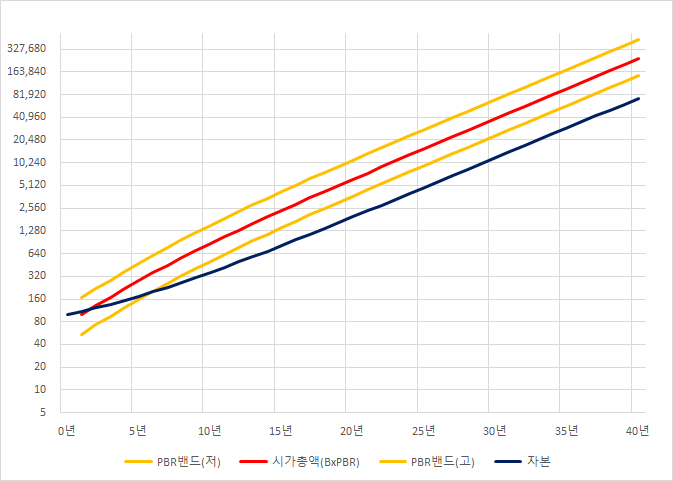
장기 성장의 초기에 있는 회사가 보여주는 전형적인 그래프.
PBR밴드의 수직이동이다.
이 경우의 투자자 수익율은,
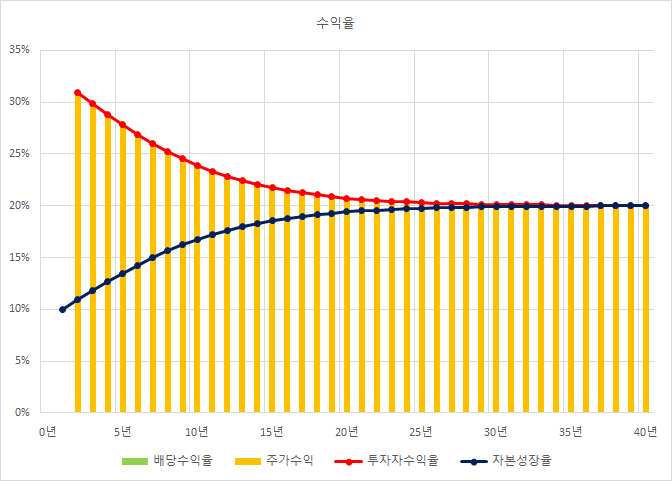
초기에 기업의 자본 성장율보다 투자자 수익율이 월등히 높다.
궁극적으로는 sROE수준(=20%)에 수렴하고.
2005년경의 LG화학의 모습이다.
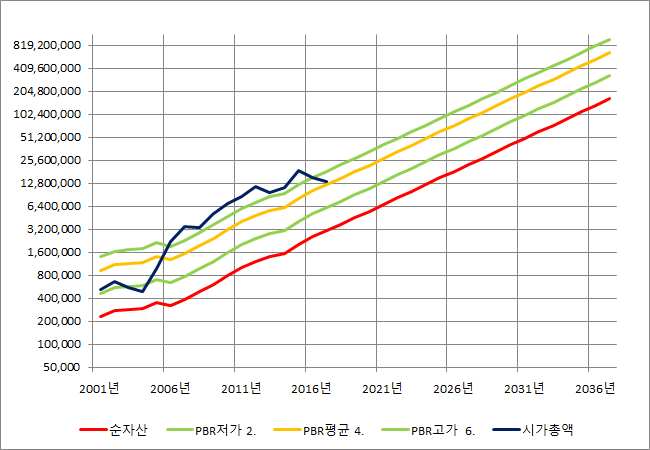
LG생활건강 리레이팅
반대로,
현재 ROE가 10%인 회사의 성장율이 5%로 줄어드는 경우를 보자.
자본의 성장율과 ROE는 5%에 수렴하게 되고,
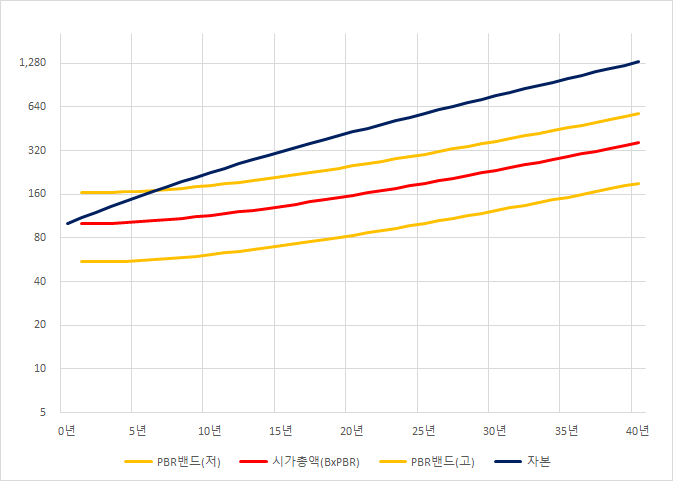
투자자의 수익은,
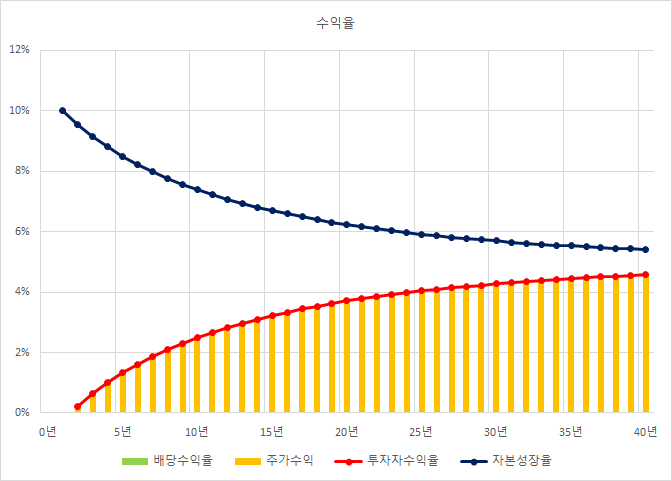
성장율 감소의 초기에 매우 낮거나,
실제로는 이전에 고평가를 조정하면서 손실을 입게 된다.
요즘 LG생활건강의 주가가 주춤하고 있는 이유.
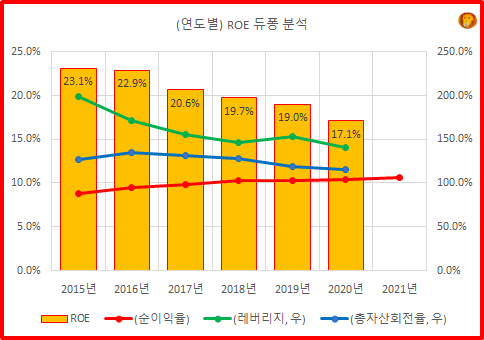
계속 성장하고 있지만,
이전에 비해서 줄어들고 있다.
덩치가 커지면 그만큼 성장이 어려워지기 때문에,
자본 재배치의 역량이 중요해진다.
외부성장을 더해야한다.
조금더 큰 변화로 보면,
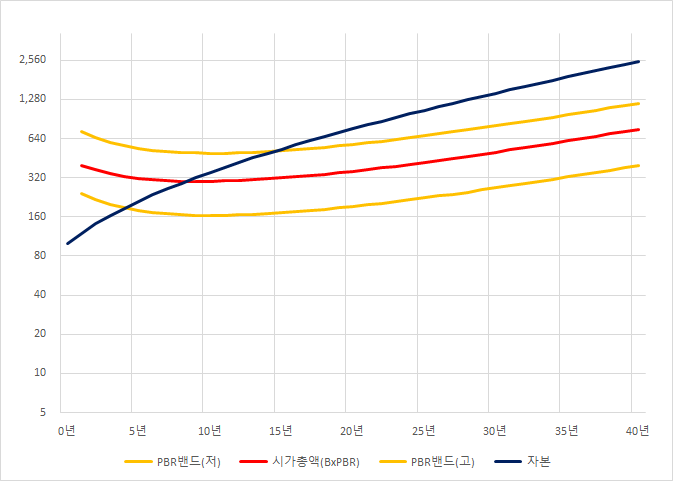
2015년의 아모레퍼시픽의 모습이다.

투자의 대상 선정 순서가 나온다.
1. ROE가 낮았던 기업이 장기적으로 고ROE회사로 변신하는 초기.
2. ROE가 지속해서 높이 유지되는 회사
이번에는 배당의 영향을 추가해 본다.
위의 경우 벌어들인 돈을 전부 기업에서 재투자를 한 경우이고,
배당을 하게 되면 ROE를 유지하기가 쉬워진다.
문제는 투자자에게 있어 배당을 받을 때 세금을 내야 한다는 점.
배당을 하지않고 꾸준히 성장해 주는 회사가 베스트인 이유다.
버핏 할배가 위대한 이유. ㅋ
지속가능한 ROE수준은 배당을 많이 할 수록 높아지게 된다.
ROE = g / (1-d)
배당을 하게 되면 투자자의 수익은 주가상승으로 인한 수익과 배당수익 두가지로 나뉜다.
몇가지 케이스를 보면 쉽게 이해될듯.

배당성향을 20%로 두면,
위에서와 달리, 지속가능한 ROE 수준이 12.5% ( =1/0.8)가 된다.
배당을 하지 않던 회사가 배당을 시작하게 되면,
그것만으로도 미래의 ROE를 높이는 효과가 있다.
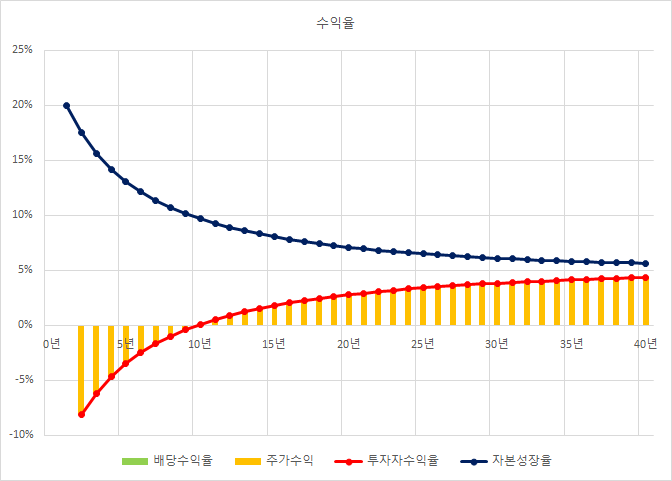
그래서 밸류에이션의 리레이팅이 있을 수 있다.
이경우에 투자자가 얻을 수 있는 수익은,
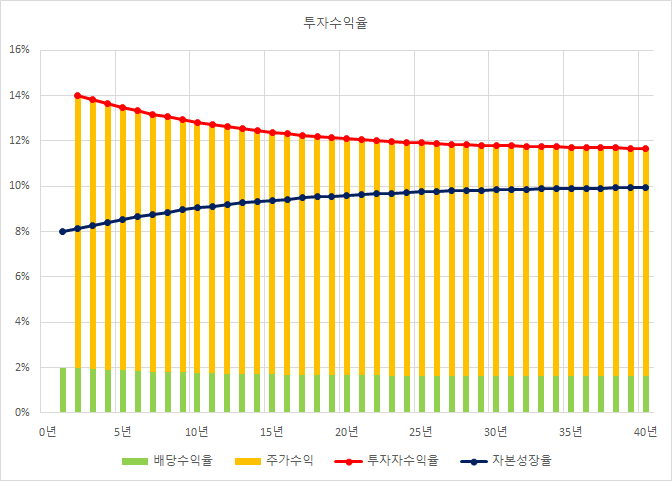
배당을 지급한 시기에는 2%이지만,
주가가 상승하면서 배당수익율이 떨어지게 된다.
실적이든, 배당이든 긍정적 변화 초기에 주가수익은 최대.
이후에는 본질적인 수준으로 돌아간다.
가정이 다소 과할 수는 있는데,
실제 현상을 잘 설명하는 모습들이 아닌가 싶다.
세금이 들어가면 배당의 효과가 더 떨어지게 되는데..
엑셀 시트 첨부할테니 이리저리 넣어보시면 인싸이트를 얻을 수 있지 않을까 싶네요.
'주식공부 > 투자원칙 철학' 카테고리의 다른 글
| 숙향의 투자 편지(81) - 2007년 말 vs 2021년 말(2) (0) | 2022.01.28 |
|---|---|
| (펌글) 버틀러 사용법 (0) | 2022.01.26 |
| (버틀러 사용법) ROE-PBR 그래프의 이해 (0) | 2022.01.26 |
| (버틀러 사용법) ROE 분석 (+ 듀퐁 분석) (0) | 2022.01.26 |
| 퀀트지표 #3 PSR(주가매출액비율) (0) | 2022.01.02 |