검색 이론 (3/3) - 검색모델 (Retrieval Models)

앞에서 문서의 색인과 대략적인 정보검색 방법을 알아봤다면,

이번에는 실제 정보검색에서는 어떠한 방법(검색모델)으로 질의와 문서의 유사도를 구하는지 알아보자.

실제 정보검색 시스템의 동작과정

대표적인 방법으로는 4가지가 있다.

 

1. 불린 모델(Boolean model)

집합에 기반하여 논리적으로 있다(True) 없다(False)를 질의문으로 검색한다.

모든 색인어들에 0과 1을 할당하고 각 Term들을 논리 연산(and, or, not)으로 연결한다.

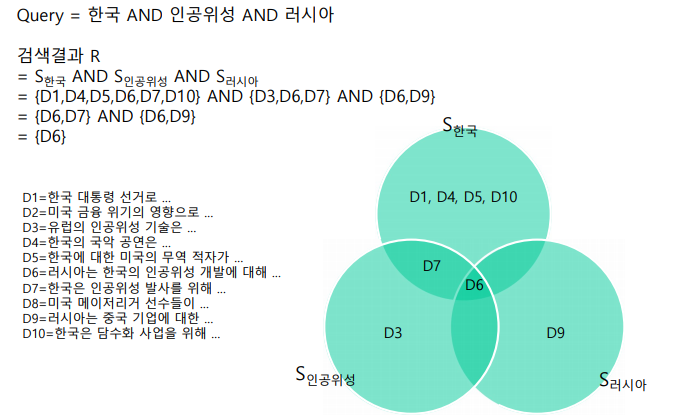
2. 벡터 공간 모델(Vector space model)

앞의 불린모델으로는 존재 여부(0 또는 1)만 알 수 있고 가중치를 계산하여 순위(Ranking)를 매길 수 없다.

그래서 가중치를 0~1 사이의 값으로 측정하는 것이 벡터 공간 모델.

각각의 n개 용어들을 n-차원의 그래프 축(벡터공간)으로 표현하고 질의문의 벡터 그래프와 문서의 벡터그래프의 유사도를 계산하는 방법.

 

2-1 코사인 유사도

코사인을 이용해서 질의 그래프와 문서 그래프의 사잇각을 구해 0~1 사이 점수를 부여하는 방법.

쉽게말해 두 벡터 그래프가 완벽하게 일치하면 1이, 직각으로 교차하면 0이 나오게 만들면 됩니다.

Cos(0') = 1

Cos(90') = 0 이므로 코사인으로 유사도를 구하면 쉽게 점수를 매길 수 있습니다.

(각도를 0~1 점수로 바꾸는 과정을 정규화, L2 Normalization 라 부릅니다)

 

우리는 여기서 Q와 D의 좌표값을 알고있고, 그 사잇각을 구해 Cos(사잇각)의 값을 구하고자 합니다.

여기서 중학교 수학에 나오는 내적값을 구하는 공식을 이용하여 Cos(사잇각)을 쉽게 구해낼 수 있습니다.

* [더보기] 내적이 뭔지 기억이 안나는데요?

내적값은 두 벡터의 방향을 무시하고, 절대적인 크기를 구하고 싶을 때 사용합니다.

위 그림과 같이 힘의 방향과 이동방향이 같다면, 저 물체를 움직이는데 사용된 일량은 [ F * S ]가 됩니다.
하지만 아래 그림과 같이 힘의 방향과 이동방향이 다르다면 일량을 어떻게 구할까요?

이때 사용하는게 [ F * S * Cos(각도) ] 가 일량이 되고, 이를 두 벡터 F, S의 내적값이라고 부릅니다.

벡터의 내적값은 온점을 이용하여 표시합니다. 단, 여기서 벡터의 방향이 반대방향인 경우 음수가 될 수 있으므로 절대값을 씌워주어야 합니다. (계산할때에는 제곱을 한 후 루트를 씌워 양수로 만듭니다.)

벡터의 내적값 = F * S * Cos(각도)

그리고 내적값은 아래와 같은 방법으로도 구할 수 있습니다.

 F * S * cos(각도)의 값과 위의 공식이 왜 같냐구요? 궁금하면 아래 링크를 통해 유도과정을 살펴봅시다.

https://sonagi87174.tistory.com/18

벡터의 내적 공식 유도하기

코사인 유사도는 두 벡터 간의 코사인 각도를 이용하여 구할 수 있는 두 벡터의 유사도를 의미합니다. 두 벡터의 방향이 완전히 동일한 경우에는 1의 값을 가지며, 90°의 각을 이루면 0, 180°로 반대의 방향을 가지면 -1의 값을 갖게 됩니다. 즉, 결국 코사인 유사도는 -1 이상 1 이하의 값을 가지며 값이 1에 가까울수록 유사도가 높다고 판단할 수 있습니다. 이를 직관적으로 이해하면 두 벡터가 가리키는 방향이 얼마나 유사한가를 의미합니다.

코사인 유사도 공식, 내적 공식에서 Cos값을 구한 것 입니다.

Q = (x,y,z)    D=(a,b,c) 라고 가정해봅시다.

분자는 백터의 내적 공식을 이용해서 같은 위치에 있는 좌표를 곱해서 더하면 됩니다.

    (x,y,z) * (a,b,c) = (x*a + y*b + z*c)

분모 |A| 는 A 벡터의 크기를 의미하며, 각 성분들을 제곱하여 더 해준 후, 마지막에 루트(sqrt)를 씌워주면 됩니다. 

    sqrt(x^2 + y^2 + z^2) * sqrt(a^2 + b^2 + c^2)

각각의 n개 용어들을 n개의 축으로 표현하고, 질의문과 문서의 그래프를 그려 사잇각을 비교한다.

2-2 이진벡터 표현

위의 코사인 유사도 예제에서는 계산의 편의성을 위해 Q와 D그래프를 이진벡터로 표현하였다.

쉽게 말해 있으면 1, 없으면 0으로 질의와 문서의 좌표(벡터 그래프)를 찍었다.

2-3 TF-IDF 벡터표현

이를 앞에서 배운 TF-IDF로 벡터를 표현하여 더 나은 유사도를 측정해보자.

단순 0,1이 아니라 TF-IDF를 이용하여 Q와 D의 좌표(벡터 그래프)를 찍어주었다. 오른쪽 아래는 유사도 값 계산